求解方程式

在《科學計算》和《數值分析》的課程當中，《求解方程式》扮演了非常重要的角色，重要的原因如下：

幾乎任何《計算問題》都可以轉換為《求解方程式》的問題。
求解方程式所用的方法，像是《優化算法、迭代法》等等，對其他計算問題非常有啟發性。

因此、在本書中，我們將從《求解方程式》開始，認識到底甚麼是《科學計算》！

您可以先試著看看用十分鐘搞懂《電腦如何解方程式》這篇十分鐘系列的文章，應該會對電腦解方程式的主題有個大致的概念，然後再回到本章中，進一步的深入電腦解方程式的實作細節！

求函數值

電腦很會計算。舉例而言、假如我們要計算下列算式

$f(x)=x^2+2x+3$

那麼只要寫個小程式，就可以輕易的算出結果！

function f(x) {
  return x*x+2*x+3;
}

就算裡面有複雜的函數，通常也可以輕易解決。

$x^t+ \sqrt{x} sin(xt)$

我們只要呼叫函式庫就行了！

function f(x,t) {
  return Math.pow(x,t)+Math.sqrt(x)*Math.sin(x*t);
}

但是、你知道怎麼求解方程式的根嗎？

像是多項式 $f(x)=x^2+2x+3$ 、多變數方程式 $x^2 y - 3xy + 5 = 0$ 、還有微分方程 $\frac{\partial^2 z}{\partial x^2}+\frac{\partial^2 z}{\partial y^2}=0$ 的根！

現在、就讓我們以程式人的直覺，先來想想到底怎麼解這些方程式。

就我能想到的方法中，第一個最簡單的方法就是《暴力法》

暴力法

怎樣暴力呢？就是把方程式裡每個變數，都從《最小到最大》算一遍，然後看看是否有符合解答的結果！

舉例而言，假如我們要求解

$x^2-4x+1=0$

而且假如我們知道《解答》在之間，那麼我們可以從 -100 到 +100，每隔 0.01 計算一次，如果有非常接近 0 的結果，那對應的 x 值就是解答了。以下是用暴力法求解 $x^2-4x+1=0$ 的程式。

檔案： bruteForce.js

function f(x) {
  return x*x-4*x+1;
}

for (var x=-100; x<=100; x+=0.001) {
  if (Math.abs(f(x)) < 0.001)
    console.log("x=", x, " f(x)=", f(x));
}

該暴力法程式的執行結果如下：

$ node bruteForce.js
x= 0.268000000113438  f(x)= -0.00017600039294918268
x= 3.7320000001131377  f(x)= -0.00017599960809100423

這種方法其實非常強大，你只要將 f(x) 寫成副程式，就可以列出任何的 f(x)=0 的解答。

像是要求方程式 $\frac{sin(x^2+2x)}{x^3} = 0$ 時，只要把函數 f(x) 換成 $f(x)=\frac{sin(x^2+2x)}{x^3}$ ，還是可以列出相當符合條件的答案！

檔案： bruteForce2.js

function f(x) {
  return sin(x*x+2*x)/x*x*x;
}

for (var x=-100; x<=100; x+=0.001) {
  if (Math.abs(f(x)) < 0.001)
    console.log("x=", x, " f(x)=", f(x));
}

上述程式的執行結果如下，只是找到了太多 f(x) 非常接近 0 的解，得要再過濾一下，讓每個區域只傳回一個最接近零的解。

D:\Dropbox\gitbook\rlab\code\solveEquation>node bruteForce2.js
x= -8.15999999988748  f(x)= -0.0009591341662344855
x= -1.999999999886453  f(x)= 4.5418779845626724e-10
x= -0.021999999886562205  f(x)= 0.0009570498717614835
x= -0.020999999886562204  f(x)= 0.0008724877870570477
x= -0.019999999886562203  f(x)= 0.000791793010175386
x= -0.018999999886562202  f(x)= 0.0007149721474338136
x= -0.0179999998865622  f(x)= 0.0006420317778407609
x= -0.0169999998865622  f(x)= 0.0005729784528665162
x= -0.0159999998865622  f(x)= 0.0005078186962133998
x= -0.014999999886562199  f(x)= 0.00044655900358536667
x= -0.013999999886562198  f(x)= 0.00038920584245704287
x= -0.012999999886562197  f(x)= 0.00033576565184219716
x= -0.011999999886562196  f(x)= 0.0002862448420616496
x= -0.010999999886562195  f(x)= 0.0002406497945106185
x= -0.009999999886562194  f(x)= 0.00019898686142551006
x= -0.008999999886562193  f(x)= 0.00016126236565015064
x= -0.007999999886562192  f(x)= 0.00012748260040146528
x= -0.006999999886562192  f(x)= 0.00009765382903460421
x= -0.005999999886562192  f(x)= 0.00007178228480751984
x= -0.004999999886562192  f(x)= 0.000049874170644996144
x= -0.003999999886562192  f(x)= 0.00003193565890213333
x= -0.0029999998865621923  f(x)= 0.00001797289112728971
x= -0.0019999998865621923  f(x)= 0.000007991977824483308
x= -0.0009999998865621923  f(x)= 0.0000019989982152556445
x= 1.134378077582987e-10  f(x)= 2.5736272459477198e-20
x= 0.0010000001134378078  f(x)= 0.000002000999118756898
x= 0.002000000113437808  f(x)= 0.000008007979511478681
x= 0.003000000113437808  f(x)= 0.00001802689287776661
x= 0.004000000113437808  f(x)= 0.00003206365843608212
x= 0.005000000113437808  f(x)= 0.00005012416268243532
x= 0.006000000113437808  f(x)= 0.00007221425914855319
x= 0.007000000113437808  f(x)= 0.00009833976815952997
x= 0.008000000113437808  f(x)= 0.00012850647659096262
x= 0.009000000113437809  f(x)= 0.00016272013762557382
x= 0.01000000011343781  f(x)= 0.00020098647050932508
x= 0.01100000011343781  f(x)= 0.00024331116030702323
x= 0.012000000113437811  f(x)= 0.00028969985765742233
x= 0.013000000113437812  f(x)= 0.0003401581785278241
x= 0.014000000113437813  f(x)= 0.0003946917039681801
x= 0.015000000113437814  f(x)= 0.0004533059798646973
x= 0.016000000113437815  f(x)= 0.0005160065166929512
x= 0.017000000113437816  f(x)= 0.0005827987892705086
x= 0.018000000113437817  f(x)= 0.0006536882365090636
x= 0.019000000113437818  f(x)= 0.0007286802611660879
x= 0.02000000011343782  f(x)= 0.0008077802295960021
x= 0.02100000011343782  f(x)= 0.0008909934715008663
x= 0.02200000011343782  f(x)= 0.0009783252796805963
x= 1.0350000001134347  f(x)= 0.0003805209790674367
x= 4.112000000113146  f(x)= -0.0008109997278331277
x= 4.96300000011343  f(x)= 0.0007453837110089035
x= 6.16000000011383  f(x)= 0.0007240722293772872

雖然這個方法很好用，但是有個重大的缺點！

這個重大的缺點就是：「暴力法的速度比較慢」！

當變數很多，或是範圍很大時，會非常的慢！

像是求解 $x^2+y^2-z = 0$ 這樣三個變數的方程式，就會需要執行 $\frac{100-(-100)}{0.001}^3$ 次函數計算，也就是八千兆次，如果有六個變數，就需要算 ( 八千兆 * 八千兆 ) 次。

所以，通常很少人用《暴力法》解決問題！

我們可以想出更好的方法，來求解方程式的根！

求解方程式的方法還有很多，像是《二分搜尋法、爬山演算法、迭代法》等等。

二分搜尋法

如果你曾經學過《演算法》，應該曾經使用過《二分搜尋法》

對於一個《連續函數》而言，假如我們知道兩個點 (a,b) ，其值 f(a)>0 且 f(b)<0 ，這樣的話勢必有一個介於 (a,b) 之間的 c 值使得 f(c)=0，假如我們每次都取，然後判斷要繼續搜尋哪一半的話，這樣我們就得到了一個《二分搜尋法》，可以較快速的找出 f(x)=0 的解答！

其想法圖示如下：

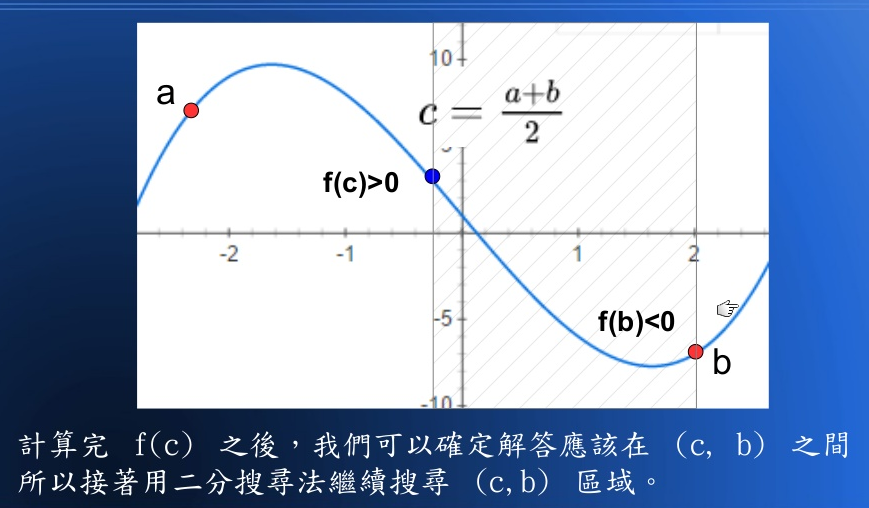
二分搜尋法求根的程式如下：

檔案： binarySearch.js

function f(x) {
  return x*x-4*x+1;
}

function bsolve(f,a,b) {
  var c = (a+b)/2;
  if (Math.abs(a-b) < 0.00001)
    return c;
  if (f(c)*f(a)>=0)
    return bsolve(f, c, b);
  else
    return bsolve(f, a, c);
}

var x=bsolve(f, 0, 1);
console.log("x=", x, " f(x)=", f(x));

執行結果：

D:\Dropbox\gitbook\rlab\code\solveEquation>node binarySearch.js
x= 0.2679481506347656  f(x)= 0.0000036088895285502076

當然，我們也可以改用另一種中間值的取法，像是用《線性內插法》在某些狀況下會更好！

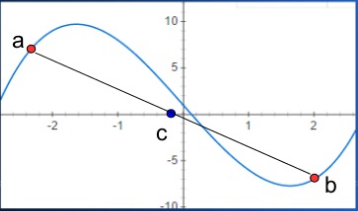
以上的這種搜尋法，不管是二分搜尋法，或者是線性內插法，速度通常都不會太慢！

如果您學過演算法中的 Big O 的複雜度概念，就會知道二分搜尋法的複雜度為 O(log n)，只是在此問題中 n 應該改為兩個邊界值之間的差，也就是 (b-a)，所以複雜度是 O(log b-a)。

但是、二分搜尋法求根的一個小問題，是必須要先找出一組 (a,b)，滿足 f(a) 和 f(b) 兩者正負號相反。

而且二分搜尋法並不是找出所有的根，而是只找出一個根，這和暴力法找範圍內全部的根有所不同！

現在、我們已經學過兩個方法了，而且這兩個方法都要先鎖定一個範圍，這種鎖定範圍的方法，稱為《界定法》 (Bracketing Method) 。

接著，讓我們看看另外一類的方法，這種方法不需要鎖定範圍，因此稱為《開放式方法》！

爬山演算法

首先，讓我們看一個最簡單的開放式方法，這個方法稱為《爬山演算法》！

爬山演算法，是通用的《優化演算法》，也就是用來尋找好的解，並不只是用來解方程的。

假如尋找的是《極大值》，那麼就是《爬山演算法》，如果尋找的是《極小值》，那麼就變成了《下山演算法》。

而且爬山演算法這類的優化算法，很容易就可以用來找方程式的解。

因為我們只要最小化絕對值 |f(x)-0| 就可以了！

爬山演算法的想法很簡單，就是先隨便選一個起點 (例如 x=0)，然後每次都比較 f(x) 和左邊的 f(x-dx) 與右邊 f(x+dx) 的值，假如左邊比較好，就往左邊走。如果右邊比較好，就走右邊。如果左邊右邊都比現在的 f(x) 差，那麼現在的 x 就是個《區域最佳解》。

假如到區域最佳解時，還沒有找到 |f(x)-0| 很接近零的解，那麼這次尋找就失敗了。

此時我們可以另選個起點繼續找，或者直接傳回尋找失敗。

以下是《爬山演算法》的程式碼，該程式碼求解方程式 $x^2-4x+1=0$ 的根。

檔案： hillClimbing.js

function f(x) {
 return -1*Math.abs(x*x-4*x+1);
}

var dx = 0.01;

function hillClimbing(f, x) {
 while (true) {
   if (f(x+dx) >= f(x))
     x = x+dx;
   else if (f(x-dx) >= f(x))
     x = x-dx;
   else
     return x;
 }
}

var x=hillClimbing(f, 0.0);
console.log("x=", x, "f(x)=", f(x));

執行結果：

D:\Dropbox\gitbook\rlab\code\solveEquation>node hillClimbing.js
x= 0.2700000000000001 f(x)= -0.007100000000000328

但是《爬山演算法》的速度並沒有很快，雖然還可以接受。

而且《爬山演算法》常常會落在《區域最佳解》出不來，因而有可能找不到《方程式的解》。

所以爬山演算法很少用來《解方程式》，而是比較常用在求解人工智慧的優化問題上！

接著、讓我們介紹另一個用來解方程式的好方法！

這也是一個開放性方法，而且不需要事先設定範圍。

這個方法稱為《迭代法》！

迭代法

話說《迭代法》，感覺非常神奇，但是說穿了很簡單！

迭代法的關鍵，可以說是一種《函數不動點》的尋找！

$x=f(x)$

$x_2 =f(x_1)$

$x_3 =f(x_2)$

...

$x_{k+1} =f(x_k)$

所謂的不動點，就是 x=f(x) 這樣一個方程式。我們從 k=0 開始反覆用 $x_{k+1} =f(x_k)$ 去找下一個 $x_{k+1}$ ，當我們找到符合 x_{k+1} =f(x_k) 的 x 時， x 基本上就定住了，這時我們找到的 x 就是 x=f(x) 的一個解答！

問題是，如果我們並非想找 f(x)=x 的解，而是 f(x)=0 的解呢？那該怎麼辦？

其實答案很簡單，只要修改方程式，想辦法讓 x 出現在其中一邊就行了。

舉例而言，假如我們想要找 f(x)=0 的解，那麼我們可以對兩邊各加一個 x ，變成 f(x)+x = x 該等式仍然會成立。這樣就可以進行迭代了！

當然、迭代的形式不只一種，對於 f(x)=0，以下都是可以用的迭代形式。

$x=f(x)+x$

$x^2=f(x)+x^2 => x=\frac{f(x)+x^2}{x}$

$3x^3=f(x)+3x^3 => x=\frac{f(x)+3x^3}{3x^2}$

$f(x)/4=0 => x=x-f(x)/4$

於是、您只要選擇一個起點，像是 x=3 ，然後開始反複套用迭代公式，看看是否會收斂就行了！

假如我們的迭代公式是 x=g(x)，那麼只要隨便選一個起點，例如 x1=3，然後用 x2 =g(x1)，x3=g(x2) … 一直算下去，直到收斂為止。

以下是一個迭代法的程式範例，用來尋找 $x*x-4*x+1$ 的解！

function f(x) { return x*x-4*x+1; }

function g(x) { return x-f(x)/4; }

function isolve(g, x) {
    console.log("x=", x);
  for (var i=0; i<100000; i++) {
    if (Math.abs(x-g(x)) < 0.001)
      return x;
    x = g(x);
      console.log("x=", x);
  }
    return x;
}

var x = isolve(g, 1);
console.log("x=", x, "f(x)=", f(x));

執行結果：

D:\Dropbox\gitbook\rlab\code\solveEquation>node iteration.js
x= 1
x= 1.5
x= 2.1875
x= 2.9287109375
x= 3.4630849361419678
x= 3.6779305535505813
x= 3.7240678179159414
x= 3.7309653577225825
x= 3.7309653577225825 f(x)= -0.0037589303643326133

這種迭代法，其實幾乎可以用來解所有的方程式，最大的問題是《可能不會收斂》！，

而且不同的迭代方法，收斂速度也常常有差異

在此我們舉一個簡單的例子，假如您想求某個數的平方根。那麼可以用下列三種的迭代算式

$x_{k+1} = \frac{3}{x_k}$
$x_{k+1} = x_k - \frac{1}{4} (x^2_k -3)$
$x_{k+1} = \frac{1}{2} (x_k + \frac{3}{x_k})$

然後實作這三種方法，程式碼如下：

檔案： iterative.js

var f1=(x)=>3/x;
var f2=(x)=>x-1/4*(x*x-3);
var f3=(x)=>1/2*(x+3/x);

x1=x2=x3=1;
for (var i=0; i<20; i++) {
  x1=f1(x1);    x2=f2(x2);    x3=f3(x3);
    console.log("x1:", x1, "x2", x2, "x3", x3);
}

執行結果

D:\Dropbox\cccwd\db\sc1\code>node iterative
x1: 3 x2 1.5 x3 2
x1: 1 x2 1.6875 x3 1.75
x1: 3 x2 1.7255859375 x3 1.7321428571428572
x1: 1 x2 1.7311742305755615 x3 1.7320508100147274
x1: 3 x2 1.7319331764233397 x3 1.7320508075688772
x1: 1 x2 1.73203504452438 x3 1.7320508075688772
x1: 3 x2 1.7320486956592371 x3 1.7320508075688772
x1: 1 x2 1.732050524625521 x3 1.7320508075688772
x1: 3 x2 1.7320507696616354 x3 1.7320508075688772
x1: 1 x2 1.7320508024902694 x3 1.7320508075688772
x1: 3 x2 1.732050806888473 x3 1.7320508075688772
x1: 1 x2 1.7320508074777203 x3 1.7320508075688772
x1: 3 x2 1.7320508075566647 x3 1.7320508075688772
x1: 1 x2 1.7320508075672412 x3 1.7320508075688772
x1: 3 x2 1.7320508075686583 x3 1.7320508075688772
x1: 1 x2 1.7320508075688479 x3 1.7320508075688772
x1: 3 x2 1.7320508075688732 x3 1.7320508075688772
x1: 1 x2 1.7320508075688767 x3 1.7320508075688772
x1: 3 x2 1.7320508075688772 x3 1.7320508075688772
x1: 1 x2 1.7320508075688772 x3 1.7320508075688772

這三種方法的收斂情形如下圖：

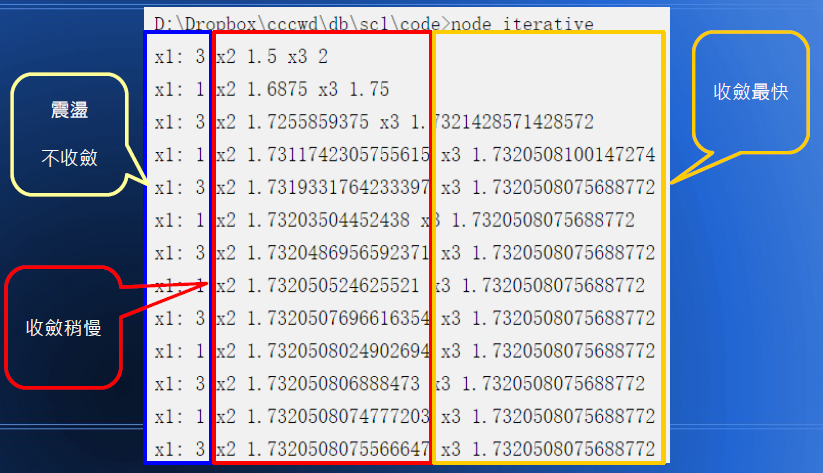
因此、好的迭代算式可以讓你上天堂，不好的迭代算式會讓你住牢房！

如果想要確定迭代法會收斂，必須要好好的設計《迭代函數》與《初始值》才行！

當然、有人可能會問，假如我想解的不是方程式，而是像下列的這種《方程組》的話，那該怎麼辦呢？

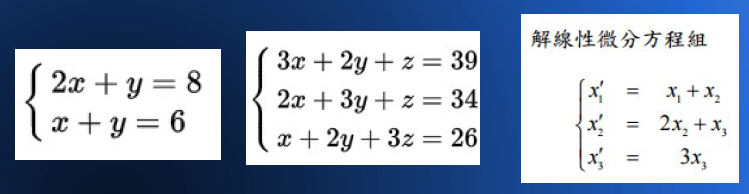
其實這個問題，只要稍微轉換一下，就可以讓《方程組變成單一的方程式》

假如您想求解下列方程組

  f(x)=0
  g(x)=0

那麼只要改寫為

$f^2(x) +g^2(x) = 0$

就可以《將方程組變成方程式》了。

只是這樣一來，線性的方程組就有可能變成了《二次的非線性方程式》

這就是，用解方程式的方法來解方程組，所需要付出的代價了。

不過迭代法確實是一個，很好的《數值方法》可以用來解很多方程式。

小結

在本章中，我們介紹了很多種方程式的求解方法，像是《暴力法、二分搜尋法、內插搜尋法、爬山演算法、迭代法》等等。

在這些方法中，筆者認為《二分搜尋法與迭代法》比較適合用在《方程式求解》這類的科學計算領域，《爬山演算法》由於速度有點慢，所以不常用，而《暴力法》則通常會更慢，所以幾乎沒有人會使用！

現在我們已經學會了求解方程式的方法，讓我們進一步來學習如何解決《線性代數、機率統計、微分方程》等等領域的問題吧！

求解方程式

求解方程式

求函數值

暴力法

二分搜尋法

爬山演算法

迭代法

小結

results matching ""

No results matching ""